Skip Navigation LinksHome » Services » Cryptography Cryptography is the practice and study of hiding information. Modern cryptography intersects the disciplines of mathematics, computer science, and electrical engineering. Cryptography follows a strongly scientific approach, and designs cryptographic algorithms around computational hardness assumptions, making such algorithms hard to break by an adversary. Such systems are not unbreakable in theory but it is infeasible to do so by any practical means. These schemes are therefore computationally secure.
Symmetric-key cryptography refers to encryption methods in which both the sender and receiver share the same key. Symmetric-key cryptosystems use the same key for encryption and decryption of a message, though a message or group of messages may have a different key than others. A significant disadvantage of symmetric ciphers is the key management necessary to use them securely. Each distinct pair of communicating parties must, ideally, share a different key, and perhaps each ciphertext exchanged as well. The number of keys required increases as the square of the number of network members, which very quickly requires complex key management schemes to keep them all straight and secret. The difficulty of securely establishing a secret key between two communicating parties, when a secure channel does not already exist between them, also presents a chicken-and-egg problem which is a considerable practical obstacle for cryptography users in the real world.
Public-key was introduced in 1976, also called asymmetric-key cryptography in which two different but mathematically related keys are used — a public key and a private key. A public key system is so constructed that calculation of one key (the 'private key') is computationally infeasible from the other (the 'public key'), even though they are necessarily related. Instead, both keys are generated secretly, as an interrelated pair. In public-key cryptosystems, the public key may be freely distributed, while its paired private key must remain secret.
In addition to encryption, public-key cryptography can be used to implement digital signature schemes. A digital signature is reminiscent of an ordinary signature; they both have the characteristic that they are easy for a user to produce, but difficult for anyone else to forge. Digital signatures can also be permanently tied to the content of the message being signed; they cannot then be 'moved' from one document to another, for any attempt will be detectable. In digital signature schemes, there are two algorithms: one for signing, in which a secret key is used to process the message (or a hash of the message, or both), and one for verification, in which the matching public key is used with the message to check the validity of the signature. RSA and DSA are two of the most popular digital signature schemes. Digital signatures are central to the operation of public key infrastructures and many network security schemes (e.g., SSL/TLS, many VPNs, etc.).
Public-key algorithms are most often based on the computational complexity of "hard" problems, often from number theory. For example, the hardness of RSA is related to the integer factorization problem, while Diffie–Hellman and DSA are related to the discrete logarithm problem. More recently, elliptic curve cryptography has developed in which security is based on number theoretic problems involving elliptic curves. Because of the difficulty of the underlying problems, most public-key algorithms involve operations such as modular multiplication and exponentiation, which are much more computationally expensive than the techniques used in most block ciphers, especially with typical key sizes. As a result, Public-key cryptosystems are commonly hybrid cryptosystems, in which a fast high-quality symmetric-key encryption algorithm is used for the message itself, while the relevant symmetric key is sent with the message, but encrypted using a public-key algorithm. Similarly, hybrid signature schemes are often used, in which a cryptographic hash function is computed, and only the resulting hash is digitally signed.
References:
Entrust: Behind the Scenes
and
Wikipedia: Cryptography
The following is description of a hybrid public-key/symmetric-key cryptology process that we have used.
| Sender | Recipient |
| Public-Key |  | | Private-Key |  | | | Public-Key |  | | Private-Key |  | |
| 1. Sign | 2. Seal | 3. Deliver |  | Hash the digital document to produce a unique digital fingerprint |  | Sign the digital fingerprint using the sender's private-key |  | Append the signed fingerprint code to the document | |  | The signed document (document with attachement) is ready to be encrypted |  | Encrypt signed document using one-time symmetric-key |  | Encrypt this one-time symmetric-key using the recipient's public-key | 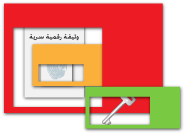 | Attach the encrypted symmetric-key to the encrypted signed document | | | Send the digital document via email, Application Programming Interface (API) Service, media...etc. | | | | 4.Accept | 5. Open | 6. Verify | | Accept the digital document | |  | Document recieved | 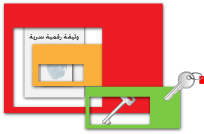 | Decrypt one-time symmetric-key using the recipient's private-key |  | Decrypt the document using the obtained one-time symmetric-key |  | Document decrypted and is ready for verification | |  | Document decrypted and is ready for verification |  | Verify the digital fingerprint using the sender's public-key |  | Rehash the digital document and compare the obtained digital fingerprint with the decrypted fingerprint | | |